Korkoa korolle laskuri
Korkoa korolle laskuri auttaa sinua laskemaan, miten sijoituksesi kasvavat korkoa korolle -periaatteella. Syötä alkupääoma, arvioitu vuosituottoprosentti, kuukausisäästösumma ja aika, niin näet, miten pääomasi kehittyy vuosi vuodelta.
Hyödynnä korkoa korolle laskuri
Arvo 5 vuoden kohdalla
Korkoa korolle ilmiö
Korkoa korolle -ilmiö tarkoittaa sitä, että vuotuisesti kertynyt tuotto lisätään aina olemassa olevaan pääomaan, jonka jälkeen se alkaa itsekin tuottaa lisää korkoa korolle tuottoa. Tämän ilmiön takia, sijoituksien arvo kasvaa ajan myötä aina vain kovemmin kiihtyvällä vauhdilla. Mitä pidempi aikajänne on kyseessä ja mitä useammin korko pääomitetaan, sitä suurempi sen vaikutus on.
Yksinkertaistettuna: ensimmäisen jakson korko lisätään pääomaan, seuraava korko lasketaan tästä suuremmasta summasta, ja niin edelleen. Pienikin korko muuttuu merkittäväksi, kun aikaa on tarpeeksi.
Miten ilmiö toimii?
- Ensimmäinen vaihe: saat korkoa alkuperäisestä sijoituksesta.
- Toinen vaihe: tämä korko lisätään pääomaan.
- Kolmas vaihe: seuraavassa kierroksessa korkoa kertyy sekä alkuperäisestä summasta että edellisistä koroista.
Ajan kuluessa tämä kertautuva vaikutus synnyttää eksponentiaalisen kasvun. Lyhyellä aikavälillä muutos voi tuntua pieneltä, mutta vuosien tai vuosikymmenten mittaan ero on valtava.
Miksi se on merkityksellistä?
Korkoa korolle -ilmiö näyttää käytännössä, että aikaa tärkeämpää tekijää sijoittajalle ei ole. Mitä aikaisemmin aloitat, sitä enemmän pääomalla on “työkaluja” kasvattaa itse itseään. Tämä tekee ilmiöstä tehokkaan keinon rakentaa varallisuutta pitkäjänteisesti ja melko vaivattomasti.
Siksi monet asiantuntijat kutsuvat korkoa korolle -ilmiötä sijoittamisen salaiseksi supervoimaksi. Se perustuu matematiikkaan, mutta vaikutuksiltaan se on puhtaasti psykologinenkin: se palkitsee kärsivällisyyden ja antaa ajan hoitaa suurimman osan työstä.

Korkoa korolle laskuri: tuottoesimerkkejä
Alla oleva esimerkki näyttää, miten sama 1 000 € kasvaa eri korkoprosenteilla, kun korko pääomitetaan vuosittain eikä lisäsijoituksia tehdä.
Oletukset: alkupääoma 1 000 €, vuosittainen pääomitus, ei lisäsijoituksia.
| Vuosi | 4 % | 8 % | 11 % |
|---|---|---|---|
| 1 | 1 040 € | 1 080 € | 1 110 € |
| 2 | 1 082 € | 1 166 € | 1 232 € |
| 3 | 1 125 € | 1 260 € | 1 368 € |
| 4 | 1 170 € | 1 360 € | 1 518 € |
| 5 | 1 217 € | 1 469 € | 1 685 € |
| 6 | 1 265 € | 1 587 € | 1 870 € |
| 7 | 1 316 € | 1 714 € | 2 076 € |
| 8 | 1 369 € | 1 851 € | 2 305 € |
| 9 | 1 423 € | 1 999 € | 2 558 € |
| 10 | 1 480 € | 2 159 € | 2 839 € |
| 11 | 1 539 € | 2 332 € | 3 152 € |
| 12 | 1 601 € | 2 518 € | 3 498 € |
| 13 | 1 665 € | 2 720 € | 3 883 € |
| 14 | 1 732 € | 2 937 € | 4 310 € |
| 15 | 1 801 € | 3 172 € | 4 785 € |
| 16 | 1 873 € | 3 426 € | 5 311 € |
| 17 | 1 948 € | 3 700 € | 5 895 € |
| 18 | 2 026 € | 3 996 € | 6 544 € |
| 19 | 2 107 € | 4 316 € | 7 263 € |
| 20 | 2 191 € | 4 661 € | 8 062 € |
Korkoa korolle kaava
Korkoa korolle -ilmiö saattaa kuulostaa monimutkaiselta, mutta sen ydin kiteytyy yhteen yksinkertaiseen kaavaan: A = P × (1 + r/n)^(n×t)
Tämä tarkoittaa käytännössä sitä, että sijoituksesi ei kasva vain alkuperäisen pääoman perusteella, vaan myös sille kertyneet korot alkavat tuottaa lisää korkoa. Toisin sanoen: raha alkaa tehdä työtä rahan puolesta.
Mitä kaava kertoo?
- P on sijoittamasi alkusumma.
- r on korkoprosentti, esimerkiksi 5 % → 0,05.
- n kertoo, kuinka monta kertaa vuodessa korko lisätään pääomaan (esim. kerran vuodessa tai kuukausittain).
- t on aika vuosina.
- A on sijoituksen loppuarvo, eli paljonko sinulla on tietyn ajan kuluttua.
Esimerkki käytännössä
Kuvitellaan, että sijoitat 1 000 € kymmeneksi vuodeksi 5 % vuosikorolla.
Kaava näyttää tältä:
A = 1000 × (1 + 0,05/1)^(1×10)
A = 1000 × (1,05)^10
A ≈ 1 628,89 €
Käytännössä siis alkuperäinen 1 000 €:n sijoitus on kasvanut yli 600 eurolla – pelkästään ajan ja korkoa korolle -ilmiön ansiosta. Jos aika olisi 20 vuotta, lopputulos olisi jo yli 2 600 €.
Miksi tämä on niin tehokasta?
Korkoa korolle -kaava osoittaa, että kaksi asiaa ratkaisee eniten: aika ja kärsivällisyys. Mitä pidempään annat sijoituksen kasvaa ja mitä useammin korkoa lisätään pääomaan, sitä jyrkemmäksi kasvu muuttuu. Siksi korkoa korolle -ilmiötä kutsutaan usein “sijoittajan parhaaksi ystäväksi”.
Korkoa korolle laskurin peruskaava
Alempana näet kaavan, jonka avulla korkoa korolle laskuri laskee sijoituksiesi tuoton. Missä:
A = loppuarvo (sijoituksen arvo korkoineen)
P = alkupääoma
r = vuotuinen korko desimaalimuodossa (esim. 0,07 = 7 %)
n = korkojen pääomitusten määrä vuodessa (esim. 12 = kuukausittain, 1 = vuosittain)
t = sijoitusaika vuosina
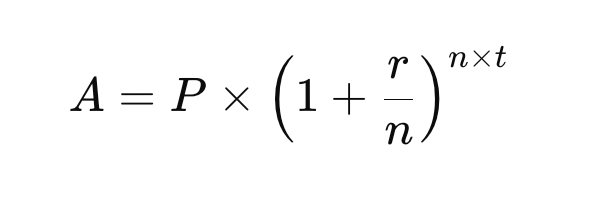
Jos teet säännöllisiä lisäsijoituksia, käytetään puolestaan laajennettua kaavaa, joka on alempana.
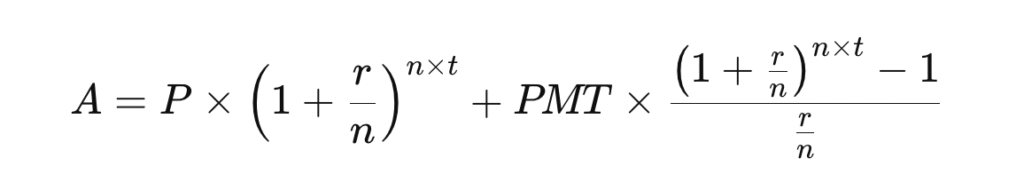
PMT = säännöllinen talletus per korkojakso (esim. kuukausisäästö)
Korkoa korolle laskuri: Usein kysyttyä
Miten korkoa korolle -laskuri toimii?
Laskuri laskee sijoituksen arvon tulevaisuudessa alkupääoman, kuukausisäästön, korkoprosentin ja sijoitusajan perusteella. Kaava huomioi, että korko pääomitetaan säännöllisesti, jolloin tuotto kasvaa kumulatiivisesti.
Mitä tarkoittaa pääomitus?
Pääomitus tarkoittaa, että ansaittu korko lisätään pääomaan — esimerkiksi kerran vuodessa tai kuukausittain. Mitä useammin korko pääomitetaan, sitä suuremmaksi sijoituksen arvo kasvaa.
Paljonko 10 000 euroa kasvaa 20 vuodessa 8 % korolla?
Jos korko pääomitetaan kerran vuodessa, 10 000 € kasvaa noin 46 610 euroon. Tämä havainnollistaa hyvin, miten aika ja korkoa korolle -vaikutus moninkertaistavat pääoman.
Mitä tapahtuu, jos en tee lisäsijoituksia?
Jos kuukausittainen säästö on nolla, laskuri näyttää, miten alkuperäinen pääoma kasvaa pelkällä korolla — eli puhtaasti korkoa korolle -ilmiön vaikutuksen.
Onko laskurin tulos veroton vai verollinen?
Laskuri näyttää tuoton ennen veroja. Jos haluat arvioida todellista nettotuottoa, voit vähentää esimerkiksi 30 % pääomatuloveron tuotosta.
Voiko laskuriin lisätä inflaation vaikutuksen?
Tällä hetkellä ei, mutta inflaation voi arvioida vähentämällä vuotuisesta tuotosta arvioitu inflaatioprosentti. Näin saat kuvan reaalituotosta eli rahan todellisesta ostovoiman kasvusta.
